How I Used the Strategy Pattern to Build a Smarter Sudoku Solver

When building the Sudoku game, one of the challenges I faced was designing a puzzle solver that was clean, modular, and easy to extend. Some puzzles can be solved with basic techniques, while others require more advanced logic or brute force.

To tackle this, I used the Strategy design pattern to create a set of pluggable solving techniques, along with dependency injection and a memento-based state manager to keep things flexible. In this post, I'll walk you through how I designed and implemented this architecture—and how it allowed me to build a solver that balances clarity with complexity.

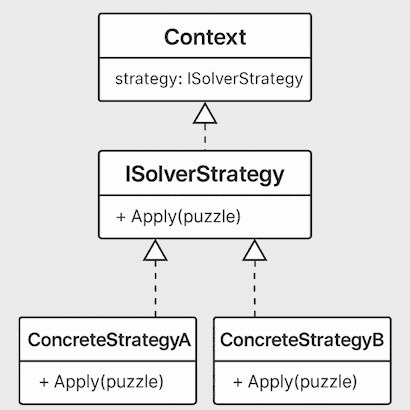
Strategy Pattern: A Perfect Fit for Sudoku

Each Sudoku strategy, like eliminating known values or identifying hidden pairs, can be modeled as a standalone component. This is exactly what the Strategy pattern is designed for.

Instead of embedding all the logic in a giant Solver class, I created a collection of strategy classes that each implement a shared interface, ISolverStrategy. This makes it easy to add, remove, or reorder strategies as the game evolves.

Puzzle Solver Architecture

The PuzzleSolver class coordinates everything, but delegates all actual solving logic to injected strategy classes.

Key Dependencies

• ISolverStrategy[]: A list of solving strategies (like “naked twins” or “single possibility”).
• IGameStateMemory: A memento-like component that stores and restores game state snapshots.

Thanks to dependency injection, these components can be swapped out in unit tests or extended with new functionality—without modifying the solver itself.

The Solving Process

SolvePuzzle()

This is the entry point. It initializes the score and runs the core loop asynchronously.

public async Task<ISudokuPuzzle> SolvePuzzle(ISudokuPuzzle puzzle)
{
    _score = 0;
    _puzzle = puzzle;

    await Task.Run(SolveLoop).ConfigureAwait(false);

    return _puzzle;
}

SolveLoop()

This is where the magic happens. The solver:

1. Saves the game state before each attempt.
2. Applies strategies using ApplyStrategies().
3. If no progress is made, it falls back to a brute-force solver.
4. If an invalid move is detected, it rolls back to the last good state.
5. Repeats until the puzzle is solved.

private void SolveLoop()
{
    var changesMade = true;

    while (changesMade)
    {
        var previousScore = _score;

        try
        {
            Save();
            changesMade = ApplyStrategies(previousScore);

            if (!changesMade)
            {
                TryBruteForceMethod();
                changesMade = true;
            }
        }
        catch (InvalidMoveException)
        {
            Undo();
        }

        if (_puzzle.IsSolved())
        {
            break;
        }
    }
}

ApplyStrategies()

This method loops through the strategy list, applying each one to the current puzzle state:

• It updates the score based on how many values the strategy resolves.
• It validates the puzzle state after each application.
• If a strategy breaks the puzzle, it throws an InvalidMoveException, triggering a rollback.

private bool ApplyStrategies(int previousScore)
{
    foreach (var strategy in strategies)
    {
        Console.WriteLine($"Solving with {strategy.GetType().Name}");
        _score += strategy.SolvePuzzle(_puzzle);

        if (!_puzzle.IsValid())
        {
            Console.WriteLine($"Failure in solving puzzle using {strategy.GetType().Name} strategy");
            throw new InvalidMoveException();
        }

        if (_puzzle.IsSolved())
        {
            break;
        }
    }

    return previousScore != _score;
}

Brute-Force Fallback

Sometimes logic just isn’t enough. If all strategies fail to make progress, the solver switches to a last-resort brute-force method.

The TryBruteForceMethod():

• Populates possible values for each cell.
• Picks the cell with the fewest options.

private void TryBruteForceMethod()
{
	Console.WriteLine($"Solving with BruteForce technique");
	_score += 5;
	_puzzle.PopulatePossibleValues();
	_puzzle.SetCellWithFewestPossibleValues();
}

It’s slower, but essential for tackling the trickiest puzzles.

State Management: Save & Undo

The IGameStateMemory component acts like an undo stack:

• Save() validates that the puzzle is valid before saving, then captures the current puzzle and score.

private void Save()
{
    if (!_puzzle.IsValid())
    {
	    throw new InvalidMoveException();
    }

    gameStateMemory.Save(new GameStateMemento(_puzzle, _score));
}

• Undo() restores the last known good state when something goes wrong.

private void Undo()
{
    var memento = gameStateMemory.Undo();

    _score = memento.Score;
    _puzzle = memento.Puzzle;
}

This allows strategies to be aggressive while giving the system a safety net when invalid moves occur.

Solving Strategies (Algorithms)

Here’s a quick overview of the types of strategies my solver uses:

🔹 Basic Elimination

• Single Value: If a cell has only one valid number, assign it.

🔹 Hidden Singles

• Singles in Column: If a number can only go in one cell in a column, assign it.
• Singles in Row: Same as above, but for rows.
• Singles in Mini-grid: Same logic, scoped to 3x3 grids.

🔹 Naked Twins

• Twins in Column / Row / Mini-grid: If two cells share exactly two possible values, eliminate those values from other cells in the same group.

🔹 Naked Triplets

• Triplets in Column / Row / Mini-grid: If three cells share three possible values, remove them from other cells in the same region.

Each of these is implemented in a separate class, making them easy to test, reuse, or extend.

Example Strategy: Single Value

Here’s a simplified version of what a strategy might look like in C#:

public class SingleValueEliminationStrategy : SolverStrategy
{
	private const int Score = 1;

	public override int Execute(ISudokuPuzzle puzzle)
	{
		var totalScore = 0;

		foreach (var cell in puzzle.GetAllCells())
		{
			if (cell.Value.HasValue || cell.PossibleValues.Length != 1) continue;

			var cellValue = int.Parse(cell.PossibleValues);
			cell.Value = cellValue;
			cell.PossibleValues = string.Empty;
			totalScore += Score;
		}

		return totalScore;
	}
}

Each strategy returns how much progress it made, which helps the solver decide whether to continue or fall back.

Error Handling & Validation

If any strategy accidentally breaks the puzzle (e.g., removes all possibilities from a cell), the solver throws an InvalidMoveException. This triggers an automatic undo from IGameStateMemory, keeping the solver resilient to bad logic.

Why This Architecture Works

✅ Separation of Concerns

• Each strategy focuses on one solving technique.
• The solver handles orchestration, not logic.
• State management is entirely decoupled.

✅ Extensibility

• Want to add a new technique like X-Wing or Swordfish? Just implement a new ISolverStrategy.

✅ Robustness

• Thanks to InvalidMoveException and Undo(), the system is resistant to strategy failures.

What’s Next

In a future post, I’ll walk through:

• How IGameStateMemory is implemented using a stack of deep-cloned puzzle states.
• How I unit-tested each strategy in isolation.

If you’re interested in seeing this solver in action, you can check out the Sudoku game here.